Physics Analysis
Exploring the phase diagram of QCD
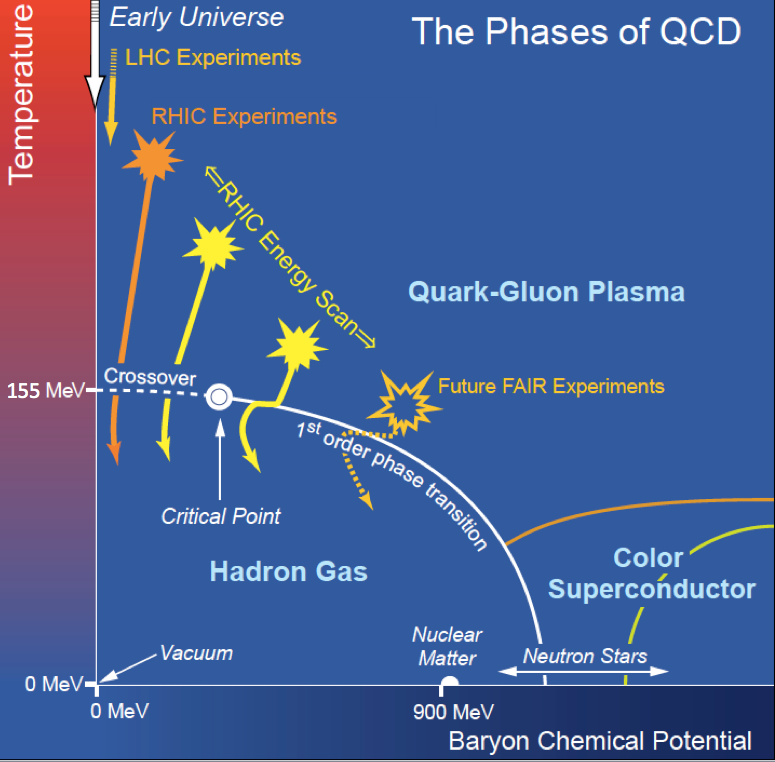 High energy heavy-ion collisions in laboratory produces a matter that can test Quantum
Chromodynamics (QCD), the theory of strong interactions (one of the four fundamental interactions in
nature), at high temperatures. One of the most exciting possibility is the existence of various
thermodynamic phases of QCD, particularly a phase of de-confined quarks and gluons (QGP) with
collective properties. The QGP phase created in laboratory is short lived ( \(10^{-22} – 10^{-23}\)
seconds) however, it mimics a longer lived plasma of free quarks and gluons in a micro-second old
Universe.
The goal of several measurements are to establish the phases of QCD and understand their properties.
The richness of the phase diagram encompasses at one end (at high temperature) the physics of early
Universe and at the other end (at high baryonic-density) the physics of astrophysical objects like
neutron star. It provides a gold mine to statistical physicists as it allows for possibility of not
only several QCD phases, but also a first order phase transition, cross over and a critical point.
Figure: from US Long Range Plan document.
High energy heavy-ion collisions in laboratory produces a matter that can test Quantum
Chromodynamics (QCD), the theory of strong interactions (one of the four fundamental interactions in
nature), at high temperatures. One of the most exciting possibility is the existence of various
thermodynamic phases of QCD, particularly a phase of de-confined quarks and gluons (QGP) with
collective properties. The QGP phase created in laboratory is short lived ( \(10^{-22} – 10^{-23}\)
seconds) however, it mimics a longer lived plasma of free quarks and gluons in a micro-second old
Universe.
The goal of several measurements are to establish the phases of QCD and understand their properties.
The richness of the phase diagram encompasses at one end (at high temperature) the physics of early
Universe and at the other end (at high baryonic-density) the physics of astrophysical objects like
neutron star. It provides a gold mine to statistical physicists as it allows for possibility of not
only several QCD phases, but also a first order phase transition, cross over and a critical point.
Figure: from US Long Range Plan document.
Apart for the signals of phase transition, it is search for this critical point which is the focus
of the Indian group. The physics of critical point, since its observations by T. Andrews, Phil.
Trans. Royal Soc., 159:575, 1869 in carbon dioxide suggests that the system undergoes large density
fluctuations when passing through this point or in its vicinity. The experimental search for the QCD
critical point by colliding Au ions hinges on the fact that matter near such a point exhibits well
understood critical fluctuations, which in terrestrial examples turn a clear liquid opalescent (like
the ones seen by T. Andrews due to large density fluctuations). The collision energy dependence of a
fluctuation observable that is particularly sensitive to the critical point is what is presented in
the current paper. As the beam energy decreases, the fluctuations near a critical point are
predicted (see Physical Review Letters 107 (2011) 052301) to make this observable swing below its
baseline value of 1.0 as the critical point is approached, then going well above, with both the dip
and the rise being greatest in head-on collisions and in analyses that record as many particles as
possible in each event.
| Observables | Moments of net-proton, net-kaon, net-charge and mean transverse momentum distributions |
|---|---|
| Groups | NISER, IITB, VECC, AMU |
Resonance and Nuclei production and understanding of hadron phase
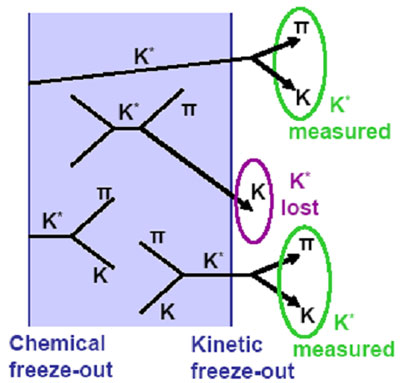 Resonances are hadrons that decay via the strong nuclear force within \(10^{−23}\) s. The first
resonance was discovered in 1960 and in 1968 a Nobel Prize was awarded to Luis Walter Alvarez for
his work, which included the discovery of many resonances. The discovery of resonances such as the
\(\Sigma(1385), K^*(892)\) and \(\rho^0\) helped confirming the quark model.
Resonances are hadrons that decay via the strong nuclear force within \(10^{−23}\) s. The first
resonance was discovered in 1960 and in 1968 a Nobel Prize was awarded to Luis Walter Alvarez for
his work, which included the discovery of many resonances. The discovery of resonances such as the
\(\Sigma(1385), K^*(892)\) and \(\rho^0\) helped confirming the quark model.
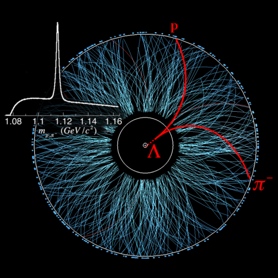
The precise particle-identification and momentum-measurement capabilities of the STAR and ALICE
experiment allow researchers to reconstruct a variety of short-lived particles or resonances in
heavy-ion collisions. These serve as a probe for in-medium effects during the last stages of
evolution of the quark–gluon plasma (QGP). For example a precise measurement of the yields (number
of particles per event) of two such resonances: \(K^*(892)^0\) and \(\phi(1020)\) have been made by
Indian
groups. Both have similar masses and the same spin, and both are neutral strange mesons, yet their
lifetimes differ by a factor of 10 (\(4.16\pm0.05\) fm/c for \(K^{*0}\), and \(46.3\pm0.4\) fm/c for
\(\phi\)). The shorter
lifetime of the \(K^0\) means that it decays within the medium, enabling its decay products (\(\pi\)
and \(K\)) to
re-scatter with other hadrons. This would be expected to inhibit the reconstruction of the parent
\(K^{∗0}\), but the \(\pi\) and \(K\) in the medium may also scatter into a \(K^{∗0}\) resonance
state, and the interplay of
these two competing re-scattering and regeneration processes becomes relevant for determining the
\(K^{*0}\) yield. The processes depend on the time interval between chemical freeze-out (vanishing
inelastic collisions) and kinetic freeze-out (vanishing elastic collisions), in addition to the
source size and the interaction cross-sections of the daughter hadrons. In contrast, due to the
longer lifetime of the \(\phi\) meson, both the re-scattering and regeneration effects are expected
to be
negligible. Hence, resonances are very good probesw of physics of hadronic phase.
| Observables | Transverse momentum distribution, rapidity density, particle ratios |
|---|---|
| Groups | NISER, IITB, IITI, IOP, PU, JU |
Jets: The important probes to the QGP
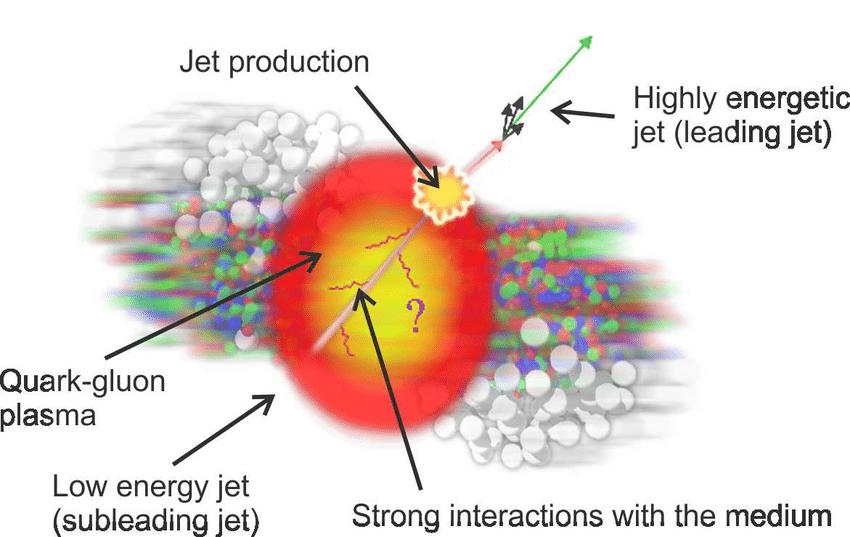

Jet is a collimated shower of particles produced from the fragmentation and hadronization of hard scattered parton (parton produced in interactions with large momentum transfer Q2) in high energy hadronic and nuclear collisions. Jet is one of the most important probes to the QGP. Experimentally jet can be measured using jet reconstruction algorithms and provides proxy for the parton from which it is produced. In proton-proton (pp) collisions jet provide a testing ground for the pQCD and non-pQCD aspects of jet production and fragmentation as implemented in the theoretical models and forms a baseline for similar measurements in proton-nucleus (p-A) and nucleus-nucleus (A-A) collisions. In the presence of QGP medium, an energetic parton loses its energy via induced gluon radiations and elastic scatterings with the medium partons. Jet production cross section and its properties are therefore modified in presence of medium compared to number of binary collision scaled pp baseline. Jet studies in A–A collisions in comparison to pp allow a better understanding of the medium induced modifications in the fragmentation of hard scattered partons and energy loss mechanisms, whereas similar studies in p–A collisions potentially reveal the effects of (cold) nuclear matter.
| Observables | Jet production cross section, jet nuclear modification factor (RAA), jet fragmentation distributions, jet shapes and jet structures |
|---|---|
| Groups | BI, VECC |
Properties of QGP through collectivity measurements
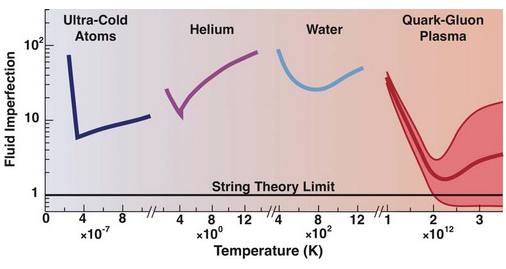
Heavy-ion collisions in the RHIC and LHC generate temperatures (T) of the order of 1012 - 1015 degrees kelvin. Under these extreme conditions, protons and neutrons melt, freeing the quarks from their bonds with the gluons leading to QGP formation. Thus, recreating in the laboratory conditions similar to those during a few microseconds old Universe. Studying such a phase and its properties tests the theory of quantum chromodynamics (QCD), provides understanding of the phenomenon of confinement, and the physics of chiral-symmetry. While the confinement tells why we observe only colourless states in the particle spectrum in nature, the chiral symmetry on the other hand describes the presence of particles like pions and mass generation of nucleons, which then accounts for most of the mass of all the visible matter. The experiment in conjunction with the theory has measured several properties of the QGP medium like the shear viscosity to entropy density \((\eta/s)\sim (1-2)1/4\pi\), stopping power also called as opacity of the medium \(\sim2-10\) GeV2/fm and diffusion co-efficient times \(2\pi T \sim 1-10\).
Out of the several properties of QGP listed above, the value of \(\eta/s\sim 1/4\pi\) led to the discovery of the emergent property of QCD matter, namely the perfect fluidity. Maxwell had realized that for a dilute gas, the shear viscosity is related to momentum transport by individual molecules and is given as \(\eta = (1/3)npl\). Here \(n\) is the density, \(p\) is the average momentum of the molecules, and \(l\) is the mean free path. As mean free path varies inversely with density, \(\eta\) to a good approximation is independent of density (one interesting consequence is that the damping of a pendulum caused by the surrounding air is independent of atmospheric pressure!). For a fixed density and temperature, as \(\eta\) is proportional to mean free path \((l)\), it will become smaller with stronger interactions among the constituents of the fluids. So, is there a limit to how small a value \(\eta\) can take up? The shear viscosity is a measure of the ability of a fluid to transport momentum from one point to another, and Heisenberg’s uncertainty in quantum mechanics puts limits the accuracy with which momentum and position can be simultaneously determined. This leads to \(pl\geq\hbar\) . Considering entropy density \(s\sim k_Bn\), the lower bound to \(\eta/s\geq \frac{\hbar}{k_B}\) . However, this simple estimate is not the complete physics story, it turns out that a precise value on the bound on the viscosity can come from string theoretical calculations using the anti-de Sitter/Conformal Field Theory conjecture. It was shown by Kovtun, Son, and Starinets (also called KSS bound) \(\eta/s\geq \frac{\hbar}{4\pi k_B}\) (modulo come corrections). The QGP fluid created at RHIC and LHC is found to have a \(\eta/s\) value close to \(1/4\pi\) (KSS bound in natural units, \(\hbar=k_B=1\) ), hence it is termed as a perfect fluid.
| Observables | Azimuthal distributions, transverse momentum distributions, nuclear modification factors |
|---|---|
| Groups | JU, NISER, GU, SINP |
Initial conditions: Angular momentum and Magnetic field effects
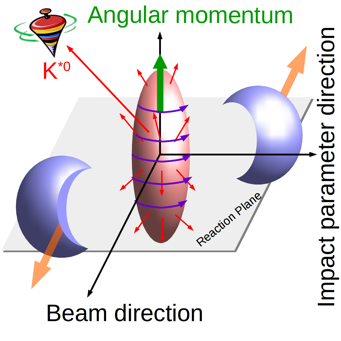
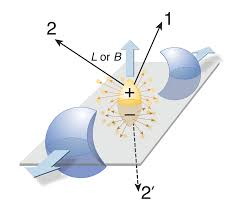
Recently, it was realized that the perfect fluid of QGP formed in ultra-relativistic heavy-ion collisions is subjected to two interesting initial conditions: (a) Angular momentum and (b) Magnetic field. Angular momentum of the order of 107\(\hbar\) is theorized to be imparted to the system through the torque generated when two nuclei collide at non-zero impact parameter with center of mass energies per nucleon of few TeV. This leads to a thermal vorticity of the order of 1021 per second for the QCD matter formed in the collisions. Further, when the two nuclei collide in the LHC, an extremely strong magnetic field of the order of 1015 tesla is generated by the spectator protons, which pass by the collision zone without breaking apart in inelastic collisions.
The effect of the angular momentum, a conserved quantity, is expected to be felt throughout the evolution of the system, the magnetic field on the other hand is transient in nature and stays for a few fm/c in time scale. Just to give an idea of the magnitude of these values, the highest angular momentum measured for nuclei ~ 70\(\hbar\) and the strongest magnetic field we have managed to produce in the laboratory is ~ 10 3 tesla. Are there experimental signatures of these phenomenally large initial conditions? The complexity enters due to the femtoscopic nature of the system formed in the heavy-ion collisions, both in space and time scales. Nevertheless, the experiment has been able to address this challenging problem.
| Observables | Angular distributions and correlations |
|---|---|
| Groups | NISER, UOR |
Small systems
| Observables | Angular distributions, Rapidity distributions, momentum distributions |
|---|---|
| Groups | UOR, BI, VECC, NISER, IITB, IITI |
Photon Multiplicity Measurements
Physics Today 56, 10, 48 (2003)
Using the measured observables in the PMD, investigations in the following broad topics of physics is pursued:
- understanding particle production mechanism (inclusive photons) and the longitudinal scaling of pseudorapidity distributions
- determination of the reaction plane and probes of thermalization via studies of azimuthal anisotropy and flow;
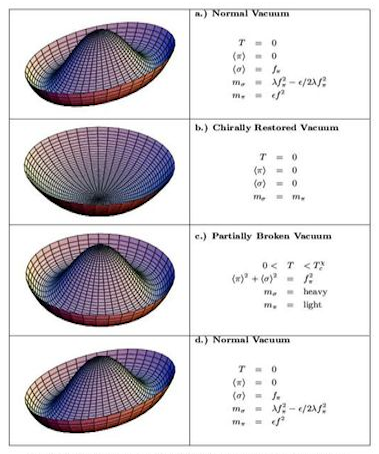
- critical phenomena near the phase boundary leading to fluctuations in global observables like multiplicity, mean transverse momentum and pseudorapidity distributions;
- signals of chiral-symmetry restoration (e.g. disoriented chiral condensates) through the measurement of charged-particle multiplicity (\(N_\mathrm{ch}\)) in a common part of phase space and study of the observables \(N_\gamma\) and \(N_\gamma/N_\mathrm{ch}\) with full azimuthal coverage.
| Observables | Spatial, Azimuthal and rapidity distributions; event-by-event multiplicity |
|---|---|
| Groups | UOR, BI, VECC, NISER, IITB, IITI |